dimecres, 30 de novembre del 2011
Més sobre dimensió fractal
Aquesta és la segona entrega... Tindrem ja la resposta? No oblides consultar aquest document.
dimarts, 29 de novembre del 2011
Dimensió fractal
La idea de dimensió la tenim clara, no? Parlem d’objectes de dimensió 0 (punts, ni llarg ni ample ni alt, només una idea), de dimensió 1 (línies, tenen llar, però no ample ni alt, només altra idea però que es veu, com la cantonada d’una habitació on es junta la paret i el sostre), de dimensió 2 (figures al pla, tenen llarg i ample, però no alt; segueix sent una idea, però que també “es veu”, com la superfície d’una taula). I, per fi, la dimensió 3, la dimensió que som capaços d’entendre perquè hi habitem, on tot té llarg, ample i alt. Existeixen altres dimensions? La ment matemàtica és capaç de moltes coses. Posem-la en marxa!
Mira aquest document
Mira aquest document
dilluns, 28 de novembre del 2011
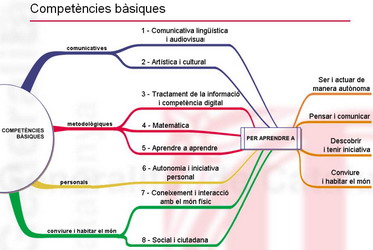
Les competències des de les matemàtiques
Des de l'assignatura de matemàtiques, el desenvolupament de les competències es pots esbossar de la manera següent:
divendres, 25 de novembre del 2011
Tutorial de Prezi
Com probablement ja sabeu, la versió gratuïta de Prezi només permet fer presentacions públiques; he creat un compte educatiu per poder treballar tots plegats. La clau d'accés la trobareu al moodle.
Ací teniu unes adreces i dos tutorials. Espere que ens siga útil a tothom.
Ací teniu unes adreces i dos tutorials. Espere que ens siga útil a tothom.
Criptografia a tres 14
Aquest és un reportatge emès al programa Tres 14 de TVE; només dura 3 minuts, i pots servir per a fer-vos una idea de com plantejar la presentació. Bona sort.
Una explicació sobre Dropbox
Aquesta presentació explica prou bé com funciona Dropbox. Si teniu preguntes, utilitzeu els comentaris o el meu correu.
Visualització del codi Cèsar
El codi Cèsar és un sistema de xifratge que desplaça les lletres segons una clau coneguda per l'emisor i el receptor. Si cada lletra (A, B, C, ...) ve reprentada per un número (1, 2, 3, ...), aquesta gràfica et pot ajudar a codificar i descodificar un missatge.
dijous, 24 de novembre del 2011
La bellesa, Documental de La 2
¿Esto es bello o no lo es? ¿La belleza es un concepto objetivo o subjetivo? ¿Esto es bello porque me gusta, o me gusta porque es bello? ¿Condiciona la moda la belleza? ¿Hay belleza moral? Luis Antonio de Villena nos ayuda en este documental a desentrañar estos interrogantes.
Punxa ací
dimecres, 23 de novembre del 2011
Activitats relacionades amb triangulacions
Les activitats fan referència al problema de la galeria d'art, també conegut com problema del museu.
Mireu aquestes activitats
Mireu aquestes activitats
Problema d'abelles
Les abelles es reprodueixen segons aquestes lleis:
Estudia com evoluciona la quantitat d'avantpassats que tenen una abella mascle i una abella femella, i quina és la proporció (quocient) entre el nombre de femelles i el nombre de mascles d'una bresca. Utilitza les gràfiques adequades.
- Una abella mascle (borinot) prové d'un ou no fecundat, doncs té mare però no pare.
- Una abella femella prové d'un ou fecundat, doncs té mare i pare.
Estudia com evoluciona la quantitat d'avantpassats que tenen una abella mascle i una abella femella, i quina és la proporció (quocient) entre el nombre de femelles i el nombre de mascles d'una bresca. Utilitza les gràfiques adequades.
French roast
Mira el vídeo. Analitza:
- La opinió inicial sobre cada personatge (aparences)
- Com actua cadascun d'ells (actituds)
- Escriu arguments per defendre el punt de vista de cada personatge (posar-te en el seu lloc)
dimarts, 22 de novembre del 2011
dimecres, 16 de novembre del 2011
dilluns, 14 de novembre del 2011
dimecres, 9 de novembre del 2011
Optimitzar triangles
El triangle té perímetre 10 cm. Pots modificar la longitud de dos costats, ja que el tercer costat està determinat pel perímetre.
- Fes que la longitud dels costat b siga 2 cm, i fes variar la longitud del costat 'a'. Quin triangle té àrea màxima?
- Ara, repeteix el procediment amb longitud de 'b' 3 cm
- Fes-ho més vegades, canviant cada vegada el valor de la longitud de 'b'.
- Quina conclusió n'extraus? Quin triangle de perímetre 10 cm té major àrea?
Optimitzar rectangles
El rectangle té perímetre 10 cm. Pots modificar la longitud de la base; l'alçària està determinada pel perímetre.
- Quin rectangle té àrea màxima?
- Fes una taula on poses almenys 20 valors de la base, el corresponent valor de l'alçària i el de l'àrea. (Una taula amb tres columnes)
- Representa gràficament les relacions base-alçària i base-àrea.
Optimitzar pentàgons
El pentàgon té perímetre 10 cm i tots els costats iguals (cada costat amida 2 cm). Pots moure els vèrtexs.
- Quin pentàgon té àrea màxima? (Ve expressada en centímetres quadrats, evidentment)
- Compara-la amb l'àrea màxima del triangle i del rectangle (tots tres tenen perímetre 10 cm, recorda-ho). Quina àrea és major?
La millor figura plana
De totes les figures planes, la figura òptima és aquella que té l'àrea màxima entre totes les figures amb el mateix perímetre, o el mínim perímetre entre totes les figures amb la mateixa àrea.
Deprés de fer l'estudi d'algunes figures (triangle, rectangle, pentàgon), ja et pots imaginar quina és la figura òptima.
Per si encara tens dubtes, pots utilitzar aquesta construcció.
No oblides fer un treball on contestes totes les qüestions plantejades i que resumisca tot el procés seguit.
Deprés de fer l'estudi d'algunes figures (triangle, rectangle, pentàgon), ja et pots imaginar quina és la figura òptima.
Per si encara tens dubtes, pots utilitzar aquesta construcció.
- Fes una taula amb el nombre de costats del polígon regular i l'àrea.
- Representa gràficament la relació.
No oblides fer un treball on contestes totes les qüestions plantejades i que resumisca tot el procés seguit.
dilluns, 7 de novembre del 2011
La ola (Die Welle)
Estem veient a la classe d'Atenció Educativa aquesta pel·lícula de Dennis Gansel del 2008.
Estaria bé fer una petita sinopsi i després escriure impressions sobre ella. Què esteu sentint? Quines emocions genera?
divendres, 4 de novembre del 2011
Matemàtiques experimentals
Buscant nous temes que podem investigar a classe he trobat aquesta adreça, que em sembla molt interessant, i que vos pot suggerir moltes línies sobre les quals treballar. Espere que us agrade.
Deures
No oblideu que és necessari practicar les coses que veiem a classe. Últims dies per poder preguntar dubtes. Farem una proveta dimecres.
- Tot a les pàgines 142, 143 i 144 i l'activitat 7.6 de la pàgina 145
- Sobre nombres irracionals, pàgines 269 a 272
Joc: qui composa el nombre?
Maria i Ximo estan jugant un joc de divisibilitat amb un conjunt de 10 targetes, cadascuna amb una xifra del 0 al 9.
Per torns cadascú tria una targeta i la col·locar a la dreta de les targetes que ja són allà.
Quan hi ha dues targetes, el número de dos dígits ha de ser divisible per 2.
Quan hi ha tres targetes, el número de tres dígits ha de ser divisible per 3.
Després de posar quatre targetes, el número de quatre dígits ha de ser divisible per 4.
I així successivament.
Perd qui no pot fer el número amb les condicions dessitjades.
- N'hi ha estratègies que ajuden a guanyar?
- Quin és el número més llarg pots fer allò satisfà les regles del joc?
- És possible d'utilitzar els deu dígits per crear un número amb les regles del joc?
- Hi ha més d'una solució?
Subscriure's a:
Missatges (Atom)